Векторная диаграмма трехфазной цепи – важный инструмент для анализа и оценки работы трехфазных систем электропитания. Построение такой диаграммы позволяет наглядно представить взаимное расположение фазных векторов напряжения и тока в цепи.
Одним из распространенных способов представления трехфазной цепи является векторная диаграмма в виде треугольника. В этой геометрической форме отображаются фазные напряжения и токи, что помогает лучше понять взаимодействие компонентов электрической цепи.
В данной статье мы рассмотрим процесс построения векторной диаграммы трехфазной цепи в виде треугольника, который поможет углубить знания в области электротехники и сделать анализ электрических цепей более наглядным и эффективным.
Как построить векторную диаграмму
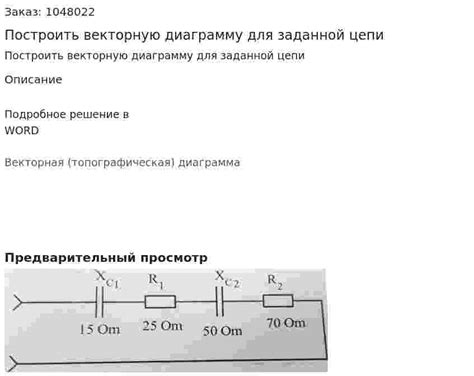
Для построения векторной диаграммы трехфазной цепи в виде треугольника необходимо выполнить следующие шаги:
- Определите направление фазовых напряжений: Необходимо определить направление фазовых напряжений и обозначить их на векторной диаграмме. Обычно используется следующая система обозначений: UAB – напряжение между фазами A и B, UBC – между фазами B и C, UCA – между фазами C и A.
- Постройте основные векторы: Постройте векторы фазовых напряжений на диаграмме, с учетом их величины и направления. Обозначьте их буквами и стрелками.
- Сложите векторы: Сложите векторы напряжений в соответствии с правилом сложения векторов. Результат сложения будет обозначать общий вектор напряжения цепи.
После выполнения этих шагов вы получите векторную диаграмму трехфазной цепи в виде треугольника, которая поможет понять взаимосвязь фазовых напряжений и токов в цепи.
Определение системы координат
Нахождение векторов фазных напряжений
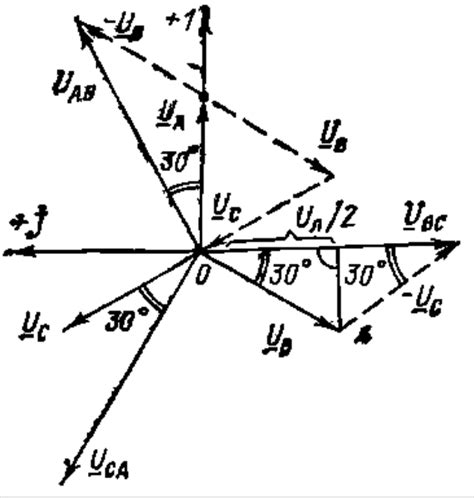
Для построения векторной диаграммы трехфазной цепи в виде треугольника необходимо знать величины фазных напряжений каждой фазы. Для нахождения векторов фазных напряжений используется формула:
Uф = U * √2 * sin(ωt ± φ)
Где:
- U - амплитудное значение фазного напряжения (например, 220 В);
- ω - угловая частота;
- t - время;
- φ - угол сдвига.
Вычисляя значения фазных напряжений для каждой фазы, мы получаем векторы фазных напряжений. Эти векторы позволяют построить треугольник напряжений на векторной диаграмме, отображающий конфигурацию трехфазной цепи.
Построение треугольника

Для построения треугольника векторной диаграммы трехфазной цепи необходимо определить модульные значения фазных напряжений и токов. Затем, используя соответствующий масштаб, откладываем векторы напряжений и токов от начала координат.
После построения векторов можно приступать к построению треугольника, соединяя концы векторов напряжений и токов друг с другом. Таким образом, получится замкнутая фигура, представляющая треугольник векторной диаграммы.
Определение величины фазного напряжения

Фазное напряжение в трехфазной цепи определяется как величина напряжения между двумя фазами электрической системы. Для сетей симметричной трехфазной системы фазное напряжение обозначается как Uф, где индекс "ф" указывает на фазу.
Величина фазного напряжения может быть рассчитана по формуле:
- Uф = Uпр / √3
Где Uпр - линейное напряжение между двумя фазами.
Значение фазного напряжения важно для расчетов мощности оборудования, согласования системы и обеспечения надежной работы трехфазных сетей.
Указание углов между векторами
Для построения векторной диаграммы трехфазной цепи в виде треугольника необходимо определить углы между векторами фазных напряжений. Угол между двумя векторами определяется по следующей формуле:
- Угол между векторами U1 и U2: α = arccos((U1·U2) / (|U1| * |U2|)), где · обозначает скалярное произведение векторов, |U| - модуль вектора U.
- Угол между векторами U2 и U3: β = arccos((U2·U3) / (|U2| * |U3|)).
- Угол между векторами U3 и U1: γ = arccos((U3·U1) / (|U3| * |U1|)).
Измеренные углы между векторами позволят построить треугольник фазных напряжений на векторной диаграмме и определить величину и фазы фазных напряжений на цепи.
Приведение диаграммы к графическому виду
После построения векторной диаграммы трехфазной цепи в виде треугольника можно привести ее к графическому виду для наглядного представления фазных напряжений и токов. Для этого необходимо провести соответствующие линии через начальные точки векторов фазных напряжений и токов. Затем можно подписать напряжения и токи в соответствующих местах на диаграмме, чтобы визуально отобразить фазные величины. Таким образом, все элементы трехфазной цепи будут наглядно представлены на графической диаграмме, что упростит анализ и понимание ее работы.
Проверка корректности построенной векторной диаграммы
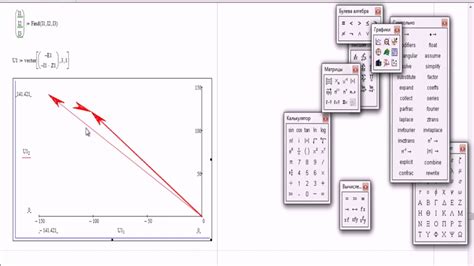
После построения векторной диаграммы трехфазной цепи в виде треугольника необходимо провести проверку корректности ее построения. Для этого следует выполнить следующие шаги:
| 1. | Проверить правильность построения фазных напряжений и токов в виде векторов, отложив их в соответствии с фазными углами. |
| 2. | Убедиться в том, что векторы напряжения и тока в каждой из фаз образуют замкнутую фигуру, соединяющую начальную и конечную точки соответствующих векторов. |
| 3. | Проверить равенство суммарных величин фазных напряжений и токов, а также их фазное соотношение в соответствии с треугольным расположением фазных векторов. |
| 4. | Проанализировать полученные результаты и убедиться в соответствии построенной векторной диаграммы реальным физическим процессам в трехфазной цепи. |
Вопрос-ответ

Как построить векторную диаграмму трехфазной цепи в виде треугольника?
Для построения векторной диаграммы трехфазной цепи в виде треугольника необходимо сначала определить величину и фазовые углы токов или напряжений каждой фазы. Затем используя методика построения векторов по длине и углам, изобразить векторы на плоскости таким образом, чтобы они образовывали треугольник. Важно учитывать их фазовые разности и соотношения между ними.
Зачем строится векторная диаграмма трехфазной цепи в виде треугольника?
Векторная диаграмма в виде треугольника позволяет наглядно представить фазовые отношения и соответствия токов или напряжений между фазами в трехфазной цепи. Это помогает при анализе симметричных и несимметричных состояний системы, определении мощности и энергии в цепи, а также при расчете параметров цепи в различных режимах работы.